距離の比による山の見え方の違い

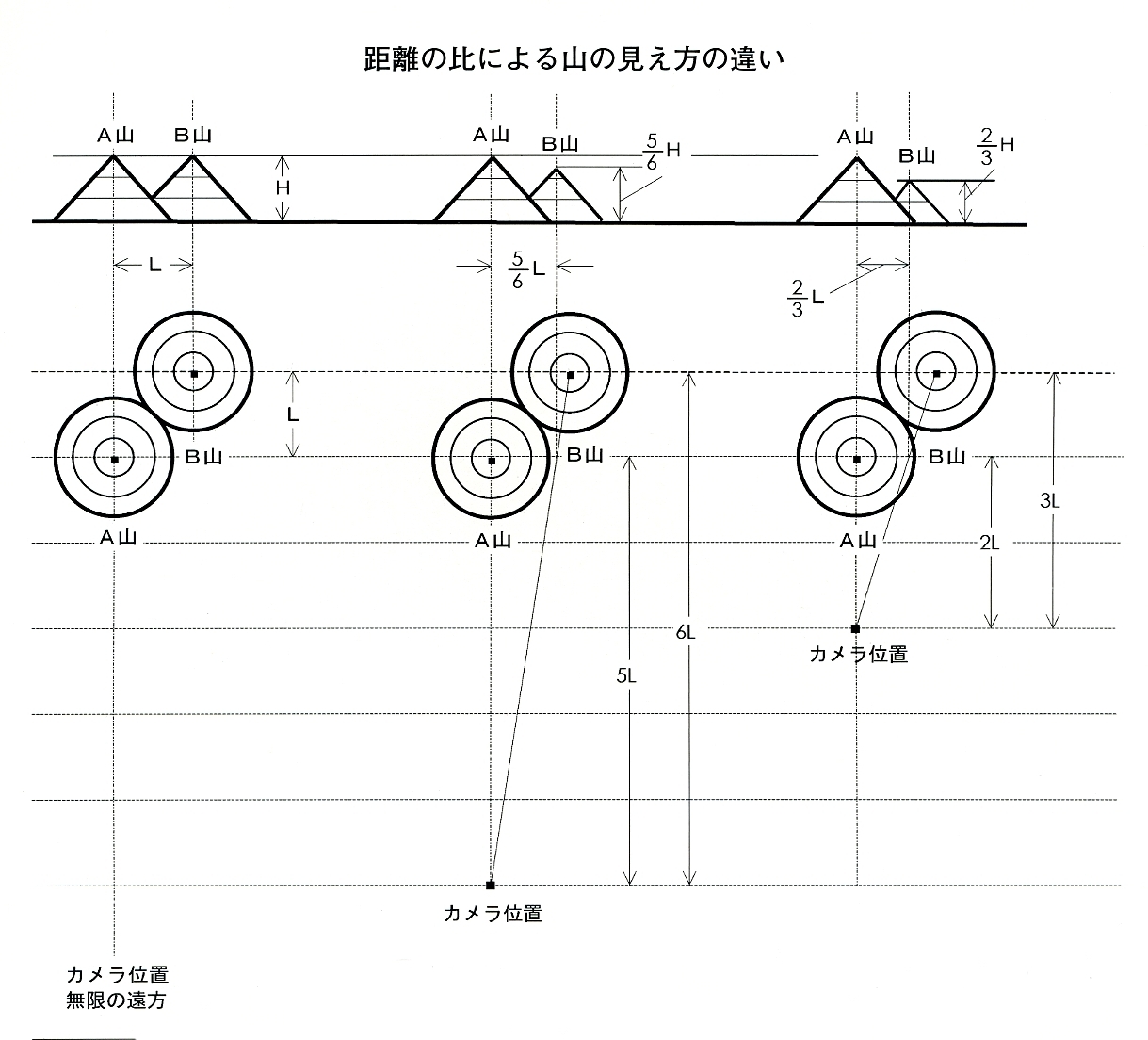
�@無限の遠方から撮ったとき。
　左の図のように、円錐形で同じ高さのＡ山とＢ山が、カメラから見て前後左右に互いにＬｍ離れて立っているとする。 距離Lmが無視できるような遠い場所から、望遠レンズでそれらの山を撮ったとする。この場合、カメラから両山までの距離は等しいと考えられるから、２つの山は同じ高さに見える。

�A中ぐらいの位置から。
　Ａ山から5Lmの距離まで近づき、Ａ山が�@と同じ大きさに写るようにズームレンズを調節した。もはや距離Lmは無視できない。
このときＢ山までの距離は6Lｍ、すなわちＡ山までの距離の５分の６倍になっている。したがって、B山の高さはＡ山の６分の５の高さに写る。同時に、水平方向の距離も縮まるから、B山はＡ山から６分の５の距離に近づいて見える。

�B近い位置から。
　さらにＡ山から2Lmの距離まで近づいたとする。B山までの距離は3Lｍ、距離の比は大きくなる。上と同様に考えて、B山の高さはＡ山の３分の２になる。当然、水平距離も３分の２に縮まる。

　以上、同じ方位から撮ったとしても、距離によって山の見え方はこのように変わる。これを見極めれば、山までの距離の違いを読みとることができ、風景を見るおもしろさが倍加する。