左の写真、雪をかぶった伊吹山と三上山が並んでいる。撮影日は１９９８年２月２日。 場所は大津市石山南郷町、俗にいう立木観音の参道からである。ただし、瀬田川鹿跳橋近くの例の石段ではなしに南郷洗堰の少し南から山手へはいって、山の中腹をたどる標高２００ｍぐらいの道である。石段を表参道とすれば、これは裏参道ということになるのだろうか。道は樹木が茂ってほとんど視界がきかないが、「六丁目」とある石標の近くだけ木立が切れてこの風景が見えた。関係地点地図

　１９９６（平成８）年１月のある日、ＪＲ琵琶湖線大津・膳所間の車窓から、雪をかぶった白い伊吹山を見た。滋賀県へ引っ越したのが１９７０年、以来２０数年そこを通りながら、初めて見る風景だった。そのときの伊吹はただ白いだけでなしに、山肌をよぎる陰影までもがはっきりと見えた。気象条件に左右されるのは当然だとしても、大津からこんなにはっきり見えるのか。それまで思っても見ないことだった。たとえ１年に数回であったとしてもこれだけ見えるとすれば、伊吹と並ぶ三上山が撮れるはずだ。

　伊吹と並ぶ三上山、理屈は簡単である。地図の上で伊吹山と三上山を直線で結び、その延長線上に立てばいいのである。その場所探しを書き出すと長くなるので省略するとして、上の写真が撮れるまでに丸２年の歳月が経過していたことになる。

　カメラをセットするとき手が震えた。まだフィルムを使っていたから、今のデジタルのようにその場で確認はできない。天気は快晴、肉眼でもはっきり見えるのだから、写ることは間違いないのだが、露出を何回測り直したことか。そうして上がってきたフィルムには、目で見たとおり２つの山がはっきり並んで写っていた。それも同じ高さで。読み進めていただければおわかりいただけるが、その２つの山が同じ高さでなければ、この項は形をなしていなかった。そういう意味でそこを参道が通っていたこと、その場所だけ木立の切れ目があったこと、すべてが神の采配であった。

２．？これはおかしい

　よくもこれだけ同じ高さで並んだものだ。よーく見ると伊吹がほんの少し高く見えないこともないが、先ず同じといって差し支えない。フィルムを見ながらふと計算してみる気になった。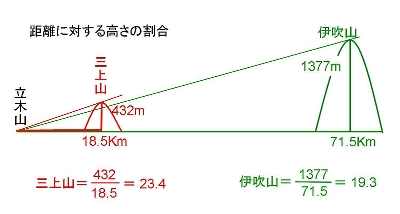

　２つの山の、立木山からの距離に対する高さの割合である。当然２つの数値はほぼ一致するはずである。しかし、出てきた結果は期待を裏切るものだった。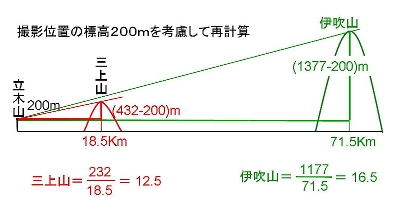
　立木山から三上山までの距離が１８．５Ｋｍ，伊吹山までが７１．５Ｋｍ。標高がそれぞれ４３２ｍ、１３７７ｍである。結果は上の通り、三上山のほうが１．２倍も高いというのである。そんなことはない、どちらもほぼ同じ高さ、どちらかといえば伊吹山がわずかに高い。三上山が高いということは絶対にない。これはおかしい。

　現場の標高を計算に入れてないことに気がついた。両山が同じ高さに見えるのは、立木山の参道から見ての話である。同じ立木山からだとして、もっと高ければ伊吹が高く見えるはずだし、位置が低ければ三上山が高く見えるはずである。標高２００ｍの参道から見て、たまたま同じ高さに見えているのである。それを計算に入れなければ結果は狂ってくるはずだ。
　立木山参道の標高を２００ｍとする、三上山の見かけの高さは２３２ｍのはずだし、伊吹山は１１７７ｍのはずだ。結果は上の通り。今度は伊吹山の方が１．３倍も高い。まだおかしい。どこかに間違いがある。

３．比叡山との場合

　話が行き詰まったときは、方向転換してみるのも一つの方法である。
　東近江市蒲生岡本町、近江鉄道の朝日大塚駅と朝日野駅の間、梵釈寺という古刹の近くから、三上山と比叡山が同じ高さに見えることを思い出した。左がその写真である。ピークが空間中の１点で合致するという珍しいケースである。関係地点地図

　同じように計算してみた。もしこちらの方がピタリと合えば、伊吹山の何かがおかしいということになる。しかし、結果は矢張り比叡山もおかしかった。三上山より高くなるのである。
　とはいえ、伊吹山、比叡山、高さも違えば場所も違う。しかし、なんとなくそこに共通点も感じられるのである。
　というのは、まずどちらも遠くのものが、数字の上では三上山より高く見えるはずにも関わらず、現実にはそれよりも低く、三上山と同じ高さにしか見えていないということである。そして、三上山に対する高さの割合をとってみると、１．３２ないしは１．３５とよく似た数値を示すことも分かってきた。これは、伊吹山だとか、比叡山だとか、特定の山の問題ではなしに、その要因がもっと大きな所にあるのではないか、そんな気がしてきたのである。

４．沈み込み量

　となればもうあれしかない。そう、「地球は丸い、遠くから近づいてくる船はマストの先から見え出す」というあの話である。小学校のときだったろうか、月食のときの地球の影が丸いなどと、例を挙げながら地球が球形であることを説明したあと、「遠くから近づいてくる船は・・・」と、さも見てきたような話を。もっともその先生自身は見たのかも知れないが、私は京都生まれの京都育ち。海など見たことネエだろうが。
　この話を聞いたのと、初めて海を見たのとどちらが先だったか。ほんまかいな。海岸で生まれたヤツは、これを毎日見とるんか・・・。この話を聞くといつも劣等感を感じていた。

　今、自分が立っている点を地球の球面のてっぺんだと考えると、周囲に見えるものはすべて遠くへ行けば行くほど沈み込んでいくということである。本来、三上山より遠くにあって高く見えるはずの山が、同じ高さに見えたのは、この沈み込みによるものである。次は、その沈み込み量の計算方法である。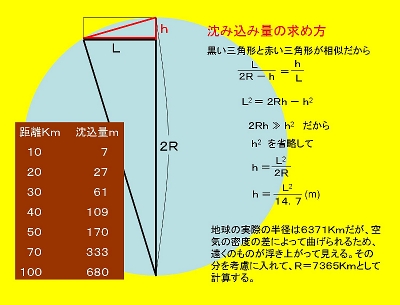

　左の図で円のいちばんテッペンが自分が立っている点。Ｒは地球の半径（Km）、Ｌは対象物（今の例で伊吹山、比叡山など）までの距離（Km）。ｈが沈込量（m）である。まじめに図をご覧くださったかたは、違和感をお持ちになるかも知れない。たとえば、対象物までの距離Ｌは、地表面で測るものなのに、図では地中の線になっていたり。確かにこういう表現をするとおかしいのだが、実際の距離は、たとえば琵琶湖の南北間の距離にしても、この図でいえば、あるかなしかの長さになり、そんなことを七面倒くさく考えることでもないのである。

　それよりも数式の下に書いてある「空気の密度の差によって曲げられるため・・・」というのがわかりにくいかも知れない。それは次のようなことである。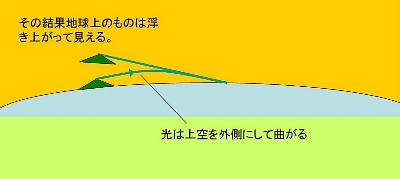　

　真空中の光の速さは１秒間に３０万Ｋｍ。真空中がいちばん速く、それ以外の物質中ではそれより遅くなる。水中では真空中の速さの３／４になる。その速さが変わるところ（水面）で光は屈折する。一般にこのように速さが変わると光は屈折する。
　我々は上空約１万ｍの空気の底に住んでいる。空気は上空の空気の重さで押さえつけられて密度が大きく、上空へ行くほど小さくなる（空気が薄くなる）。空気中の光の速さは空気の密度が大きいほど遅くなる。すなわち地上に近いほど遅く、上空へ行くほど速くなる。このため光は上空を外側として曲がる。
　たとえば夏の暑い時期、道路で見られる逃げ水、冬の琵琶湖などで見られる蜃気楼、朝夕の太陽が上下に圧縮されたような楕円に見えること、すべてこの理屈によるものである。

　ということなんだが、計算は中学か高校の１年ぐらいの数学だが、そんなことはどうでもいいし、実際の沈み込み量を左下に上げておいたからそれを参考にしてもらえばいい。いずれにしてもけっこう大きいもんだとの思いをもたれることだろう。５０Ｋｍ離れて１７０ｍも沈み込むのだから。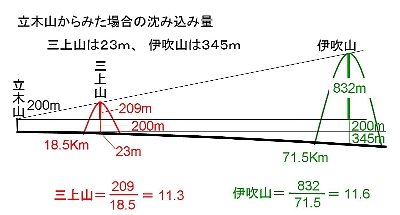

　以上のことを使って、三上山と伊吹山の関係を確認してみよう。立木山から三上山までの距離が１８．５Ｋｍ、それに対する沈み込み量が２３ｍ。７１．５Ｋｍの距離にある伊吹山は、なんと ３４５ｍも沈み込んでいる。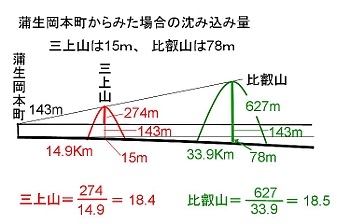
　以上、上の図より、立木山から見て、三上山と伊吹山が同じ高さに見えることが納得できる数値が出た。要するに、立木山からは三上山が２０９ｍ、伊吹山が８３２ｍの山として見えていたのである。

　もちろん比叡山との関係もピシャリ、文句なしの数値になることはいうまでもない。
　以上、山の高さを比べることで地球が丸いことを見てきたわけだが、どこかの会計報告をきいているようで、本当の丸さが実感できない。第２部ではその丸さを目で見ていただこう。

第２部　琵琶湖湖岸から

５．湖上に引く１本の線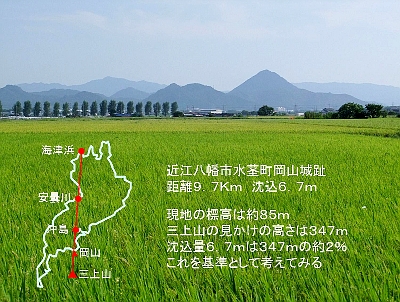

近江八幡市長命寺あたりから湖岸道路を南下する。初めての信号が「湖岸白鳥川」。そこを越えて少し行くとちょっとした峠で岡山を越える。峠左に「岡山城跡」の碑がたっているが、車からはほとんど見えない。それよりも下りになって左に見えるこの風景の方が印象に残る。
　これは岡山城址のすぐ下、三上山から９．７Ｋｍの地点から見たものである。もちろん沈み込んで見えているのだが、その量は７ｍ弱。実際の高さの２％ほどである。だからそれは無視をして、いちおうこれを三上山本来の姿として考えてみる。
　地図にあるように、三上山と湖北海津浜とを直線で結ぶ。その間に私が撮影ポイントとしている地点が４箇所含まれる。上の写真の岡山、沖島、高島市安曇川の湖岸、それと海津浜である。
　ここで上の岡山からの写真を基準として、各地点での沈み込みを比較してみよう。当然のことながら、遠くへ行けば三上山は小さく見えるようになる。それを比較して沈み込みを云々することは意味をなさない。望遠レンズで拡大して、それぞれを岡山から見る三上山の上半分の大きさに統一して比較することとする。 関係地点地図

６．沖島から

　沖島から見た三上山である。近江八幡市長命寺の沖に浮かぶ。写真は島内、沖島小学校近くからの撮影である。左の濃い島影が長命寺山のすそ。右が岡山、バックの山は金勝山系である。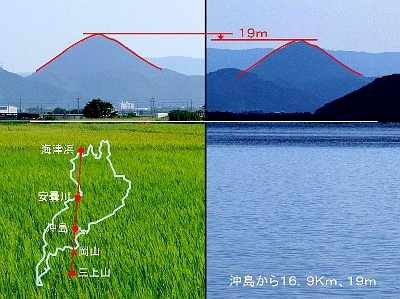
　さて私たちは、この写真を見る限り、ああ三上山が写っているぐらいの反応をするだけである。

　左は上の写真の白枠部を切り取り、岡山城址から撮った写真と並べたところである。厳密にいうと岡山城址からの写真も若干の沈み込みがあるわけだが、それは無視することとする。沖島は三上山から１６．９Ｋｍの距離にあり、１９ｍほどの沈み込みが計算できる。しかし、肉眼で見る限り三上山が沈み込んでいるという実感はない。

７．高島市安曇川から

　萩の浜から湖岸道路を北上すると、安曇川の少し手前で新金丸橋という橋を渡る。小さな入江にかかっており水辺に木が生えていたりして、叙情的な雰囲気の所である。写真はその橋の上から見た三上山である。例によっていちばん手前に沖島が見え、それに重なって岡山が見える。撮影場所が完全に一直線上ではないから、岡山の位置が少しずれているが、ほぼよく似た位置関係である。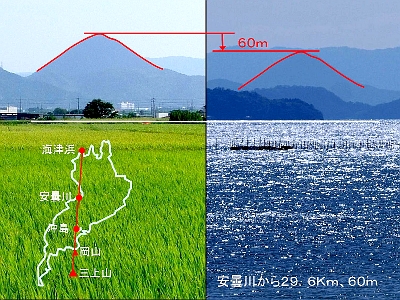

　ここまで来ると、岡山からの写真と比較して、明らかな沈み込みが感じられる。
　赤線の山形は左右同じである。上で切り抜いた写真を拡大させて、山の上半身を赤線に合わす。その後水平線を左の写真（岡山からの写真）の推定水平線に合わす。結果としては、望遠レンズで撮影したのと同じことになる。

８．海津浜から

　さて海津浜である。琵琶湖の水辺に立って、三上山が見える最遠の地である。距離４６．３Ｋｍ。はるばる来たという感がする。対岸は安曇川デルタ、三上山の右下に新旭風車村の風車が見えている。このあたりまで来ると、先ず意識せずに三上山を発見することは不可能である。見えるはずだと思って初めて見える。そのレベルの見え方である。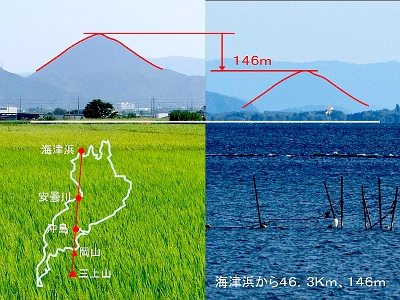

　沈込み量１４３ｍ。これはちょっとやそっとの量ではない。 距離が遠いから当然山は小さくなる、と同時におよそ半分ほどが水平線下に没しているのである。見えているのは上半身だけ。見通しのいい日にぜひ一度現場に立っていただきたい。

９．まとめ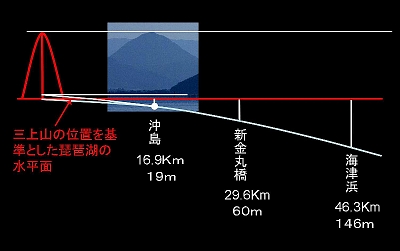

　琵琶湖の湖面を通して三上山が沈み込んでいくことは、いま見ていただいたとおりで、あとは蛇足である。
　赤い線が三上山の位置を基準とした水平線である。沖島に立つとき、基準線よりは１９ｍ下がった（この図でいえば傾いた水平線）の上に立つわけである。しかし私たちは、その傾いた水平線が真の水平線だと受け取る。結果傾いた分だけ足下が見えなくなるという勘定である。

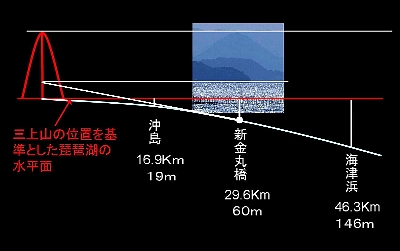
　理屈はいっしょだが、この図がいちばん見やすいかも知れない。傾いていけば行くほど三上山の足下が見えなくなっていくのである。ところが自分ではその傾きが見えないから、山全体が沈み込んでいくと感じるのである。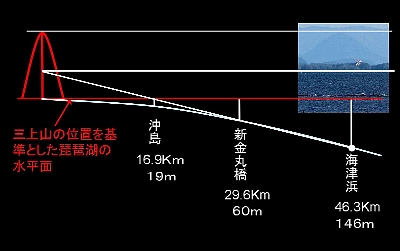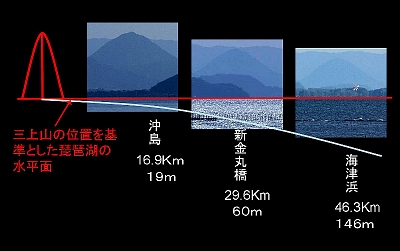

　理屈をいえば上の３つ図のように三上山の足下が見えなくなるだけの話なのだが、何度もいうが、自分が立っている場所が絶対的な水平線と感じるから、結果として左の図のように三上山が沈み込んでいくように感じるのである。

最後にもう一枚

１０．乗鞍岳から

　ここにもう１枚の写真がある。撮影位置は、福井県との県境・乗鞍岳（８６５ｍ）。麓の在原集落からの林道の８合目あたり、標高７００ｍぐらいの地点である。偶然の結果だが、ここが今まで見てきた三上山と海津浜を結ぶ直線をさらに延長した地点だった。関係地点地図。
　海津浜は手前の山の陰に隠れて見えない。その向こう右から突き出た半島が、安曇川のデルタである。　

　この項で考えてきたことは、沖島、安曇川、海津浜とすべて撮影場所がの湖岸であった。しかし、今度は７００ｍの高さがある。もちろん高くなった分、遠くまで見通せるのだが、いろいろと考えてみると、そもそも水平線とはなんぞやという問題にぶつかる。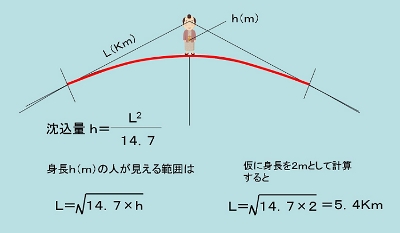
　上空を見上げると太陽も、月も、星もすべて無限の遠方にある。海岸に立ってみるとき、太陽も月も水平線から昇る。あたかも水平線は無限の遠方にあるかのように感じる。しかし、太平洋のまん中で水泳をしていて目を水面ギリギリにおいたとき、周囲はどこまで見えるのだろうか。そんなに遠方まで見えないはずである。おそらく数１００ｍ、場合によっては１００ｍ未満の場合だってあり得るのではないか。
　じゃ、身長２ｍの人（そんな人は滅多にいないが、いたと仮定して）が海岸の波打ち際に立って海面を見るとき、沖合何Ｋｍぐらいまで見通せているのだろうか。

　左の図は、上で見てもらった沈み込み量を考える図と同じである。上で考えたときは、自分の位置を基準としてＬ（Ｋｍ）離れたときにｈ（ｍ）沈み込むと考えた。今自分の身長を沈み込みと考えて、見渡せる海は半径Ｌ（Ｋｍ）だと考えているだけである。自分の身長を２ｍとすれば、５．４Ｋｍこれが水平線までの距離である。当然、自分の身長が高くなれば、見通せる範囲は広がっていく。自分の身長には限度があるから山に登れば見渡せる範囲は広がっていく。

　左は上の写真を関係箇所だけトリミングしたものである。上下の中程を横切るのが、安曇川デルタ。その向こう左に見えるのが沖島。そして面白いことに海津ではほとんど見えなくなっていた岡山がここに来て再び見えているということ。さらに、三上山そのものも海津からとは大違い、本来の姿を見せている。撮影位置の高さの効果である。

　三上山からここまでの水平距離（水平という言葉のあいまいさが気になるが、ちょっと別においておいて）が５２．８Ｋｍ、それに対する沈み込み量は１９１ｍである。１９１ｍの山のてっぺんに立てば三上山の麓まできっちり見えるということである。乗鞍岳での撮影位置はおよそ７００ｍ、そこから見渡せる地平線は１０１Ｋｍ。三上山までの距離の約２倍、三上山が安定した姿で見えるのは当然の理である。

　立木山からの伊吹を撮るまでは、地球が丸いなんてことはよその国の話だと思っていた。しかし、地球レベルから見ればほんの小さな琵琶湖でもそれが見えるのである。地球はやっぱり丸かった。